Difference between revisions of "Case Studies"
(Added picture) |
|||
| Line 20: | Line 20: | ||
==== Keywords ==== | ==== Keywords ==== | ||
CMB temperature fluctuations, excursion sets, Betti numbers, relative homology, testing for non-Gaussianities. | CMB temperature fluctuations, excursion sets, Betti numbers, relative homology, testing for non-Gaussianities. | ||
| + | |||
| + | == Dynamics on networks: TDA of contagion maps for examining spreading processes on networks == | ||
| + | |||
| + | ==== Introduction ==== | ||
| + | Spreading dynamics on networks is a phenomenon with widespread applications ranging from biological epidemics to collective social processes. Two classes of networks are to be contrasted: geometric networks, in which nodes lie in a metric space and are connected by short-range edges constrained by the nodes' location, and non-geometric networks, whose edges are not constrained by distances between nodes. It is fundamental to question the extent to which the dynamics of for instance contagions on a geometrically embedded network follows the underlying low-dimensional structure, in particular for networks including non-geometric edges. Two different characterizations of contagions exist: wavefront propagation (WFP) and the appearance of new clusters (ANC) that are spatially distant. Long-range transportation networks provide can, for example, cause ANC, which can be observed in modern biological epidemics. | ||
| + | |||
| + | ==== The study ==== | ||
| + | |||
| + | ==== Keywords ==== | ||
== References == | == References == | ||
<references />__FORCETOC__ | <references />__FORCETOC__ | ||
Revision as of 19:35, 16 May 2019
On this page multiple recent research studies are described, all of them applying methods from computational topology in different forms. Throughout, a short introduction to the research field background is given, followed by a description of the employed computational topology approach including the most important conclusions.
Astrophysics: Unexpected topology in the Cosmic Microwave Background
Introduction
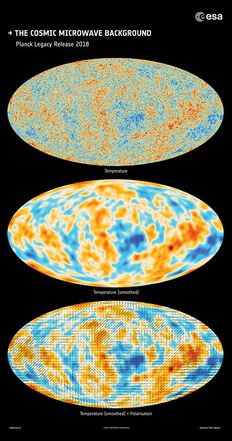
Though very homogeneous, the Cosmic Microwave Background (CMB), i.e., the electromagnetic radiation filling all space that is a remnant from an early stage of the universe, shows tiny temperature fluctuations. They have been measured in detail for instance via the Planck satellite and are believed to be generated by quantum fluctuations of matter, which subsequently expanded immensely within an inflationary phase. In inflationary theories the universe itself expanded right after the Big Bang to the size of today's observable universe, starting at a size numerous orders of magnitude smaller.
A standard cosmological paradigm is provided by the [math]\Lambda[/math]CDM model, which takes into account a cosmological constant ([math]\Lambda[/math]) and cold dark matter (CDM). By today, the CMB is the most important observational probe for the [math]\Lambda[/math]CDM model's validity. Namely, the [math]\Lambda[/math]CDM model together with inflationary theories predict the CMB temperature fluctuations to be realizations of a homogeneous and isotropic Gaussian random field. While it has largely been agreed upon that the CMB exhibits characteristics of a homogeneous and isotropic Gaussian field, there are lingering doubts.
The study
The topology of excursion sets of maps of the CMB temperature fluctuations is studied in Pranav et al 2018[1], in particular analyzing Betti numbers which quantify the number of connection components and holes. CMB maps observed by the Planck satellite are compared to simulated maps generated according to the theoretical [math]\Lambda[/math]CDM paradigm of cosmology with Gaussian distributed fluctuations.
An important ingredient of their study is that the CMB maps observed are incomplete due to inter alia bright point sources and other extended foreground objects like the milky way. A rigorous method to account for this is the introduction of masks and eventually the introduction of relative homology groups.
Statistical tests such as a parametric [math]\chi^2[/math]-test reveal differences in Betti numbers between observations and simulations with deviations up to [math]3\sigma[/math] to [math]4\sigma[/math]. The authors come to the conclusion, that "beyond the trivial possibility that this may still be a manifestation of an extreme Gaussian case, these observations may motivate to look at primordial non-Gaussianities."
Keywords
CMB temperature fluctuations, excursion sets, Betti numbers, relative homology, testing for non-Gaussianities.
Dynamics on networks: TDA of contagion maps for examining spreading processes on networks
Introduction
Spreading dynamics on networks is a phenomenon with widespread applications ranging from biological epidemics to collective social processes. Two classes of networks are to be contrasted: geometric networks, in which nodes lie in a metric space and are connected by short-range edges constrained by the nodes' location, and non-geometric networks, whose edges are not constrained by distances between nodes. It is fundamental to question the extent to which the dynamics of for instance contagions on a geometrically embedded network follows the underlying low-dimensional structure, in particular for networks including non-geometric edges. Two different characterizations of contagions exist: wavefront propagation (WFP) and the appearance of new clusters (ANC) that are spatially distant. Long-range transportation networks provide can, for example, cause ANC, which can be observed in modern biological epidemics.
The study
Keywords
References
- ↑ PRANAV, Pratyush, et al. Unexpected Topology of the Temperature Fluctuations in the Cosmic Microwave Background. arXiv preprint arXiv:1812.07678, 2018. https://arxiv.org/abs/1812.07678