Case Studies

On this page multiple recent research studies are described, all of them applying methods from computational topology in different forms. Throughout, a short introduction to the research field background is given, followed by a description of the employed computational topology approach including the most important conclusions.

The introductory material at the beginning of each section mainly summarizes information given in the cited articles, respectively.

Astrophysics: Unexpected topology in the Cosmic Microwave Background

The anisotropies in temperature and polarization of the cosmic microwave background, or CMB, as observed by ESA’s Planck mission. Picture taken from the ESA webpage.

Introduction

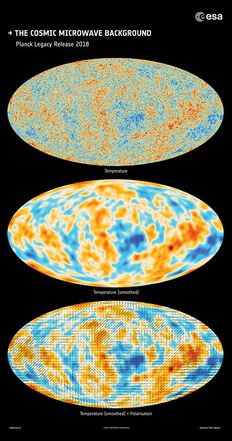
Though very homogeneous, the Cosmic Microwave Background (CMB), i.e., the electromagnetic radiation filling all space that is a remnant from an early stage of the universe, shows tiny temperature fluctuations. They have been measured in detail for instance via the Planck satellite and are believed to be generated by quantum fluctuations of matter, which subsequently expanded immensely within an inflationary phase. In inflationary theories the universe itself expanded right after the Big Bang to the size of today's observable universe, starting at a size numerous orders of magnitude smaller.

A standard cosmological paradigm is provided by the [math]\Lambda[/math]CDM model, which takes into account a cosmological constant ([math]\Lambda[/math]) and cold dark matter (CDM). By today, the CMB is the most important observational probe for the [math]\Lambda[/math]CDM model's validity. Namely, the [math]\Lambda[/math]CDM model together with inflationary theories predict the CMB temperature fluctuations to be realizations of a homogeneous and isotropic Gaussian random field. While it has largely been agreed upon that the CMB exhibits characteristics of a homogeneous and isotropic Gaussian field, there are lingering doubts.

The study

The topology of excursion sets of maps of the CMB temperature fluctuations is studied in Pranav et al 2018, in particular analyzing Betti numbers which quantify the number of connection components and holes. CMB maps observed by the Planck satellite are compared to simulated maps generated according to the theoretical [math]\Lambda[/math]CDM paradigm of cosmology with Gaussian distributed fluctuations.

An important ingredient of their study is that the CMB maps observed are incomplete due to inter alia bright point sources and other extended foreground objects like the milky way. A rigorous method to account for this is the introduction of masks and eventually the introduction of relative homology groups.

Statistical tests such as a parametric [math]\chi^2[/math]-test reveal differences in Betti numbers between observations and simulations with deviations up to [math]3\sigma[/math] to [math]4\sigma[/math]. The authors come to the conclusion, that "beyond the trivial possibility that this may still be a manifestation of an extreme Gaussian case, these observations may motivate to look at primordial non-Gaussianities."

Keywords

CMB temperature fluctuations, excursion sets, Betti numbers, relative homology, testing for non-Gaussianities.

Dynamics on networks: TDA of contagion maps for examining spreading processes on networks

The London Underground. Public domain picture taken from Wikipedia.

Introduction

Spreading dynamics on networks is a phenomenon with widespread applications ranging from biological epidemics to collective social processes. Two classes of networks are to be contrasted: geometric networks, in which nodes lie in a metric space and are connected by short-range edges constrained by the nodes' locations, and non-geometric networks, whose edges are not constrained by distances between nodes. It is fundamental to question the extent to which the dynamics of for instance contagions on a geometrically embedded network follows the underlying low-dimensional structure, in particular for networks including non-geometric edges. Two different characterizations of contagion spreading exist: wavefront propagation (WFP) and the appearance of new clusters (ANC) that are spatially distant. Long-range transportation networks can for example cause ANC, which can be observed in modern biological epidemics.

Watts threshold model is a suitable model of social contagions, in which the dynamics at any node depends on the states of all neighbouring nodes. Importantly, depending on a chosen threshold for adopting a social contagion WFP can dominate ANC and vice versa.

The study

The spreading dynamics of complex contagions in different Watts threshold models (WTM) on noisy networks with non-geometric edges are studied in Taylor et al 2015. So-called WTM maps are introduced, mapping a node of the network to its activation time in individual realizations of different initial contagion seeds. Bifurcations in WFP and ANC dynamics are analyzed by examining data that are generated by several contagions in a WTM on both, noisy ring lattices and a transit system in London.

Different WFP and ANC regimes are identified for both networks, while the underlying manifold structure can be recovered in terms of its topology, geometry and dimensionality if WFP (strongly) dominates, even in the presence of many non-geometric edges. The latter result is obtained via a Pearson correlation coefficient and via a computational topology approach to the WTM maps by means of investigating the dominating persistent homology classes in Vietoris-Rips complexes. Additionally, a variant of the dimension-reduction algorithm called Isomap is constructed. A comparison to the other regimes in the model's bifurcation diagram of WFP and ANC dynamics is given, highlighting the influence of noisy edges on contagion spreading within networks.

Eventually, the authors strengthen that their "methodology of constructing and analysing contagion maps has important implications not only for the analysis, modelling and control of contagions, but also for other dynamics that can be used to construct filtrations of networks."

Keywords

Contagion spreading, Watts threshold model, contagion maps, Vietoris-Rips complexes, persistent homology, Isomap, London transit network

Material science: Persistent homology for medium-range order in the glass

Schematically drawn, crystalline structures (left) are characterized by long-range order, while amorphous structures (right) do not exhibit this type of order. Picture taken from monq.com.

Introduction

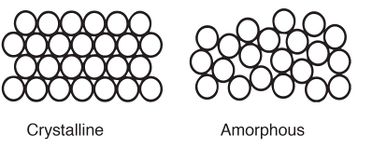
Medium-range order (MRO), i.e. the larger-scale structures beyond neighbouring atoms, plays a much more dominant role in the amorphous structures of glasses than short-range order (SRO), long-range order (LRO) being absent. Although inter alia diffraction analyses yielded evidences for the existence of MRO in these materials, their geometric origins in many-body configurations are not clearly understood such as the "periodicity" of LRO of the "chemical or packing order" of SRO.

Methods employed to date, such as angle distributions and statistics of topological quantities, are often restricted to [math]m(\leq 4)[/math]-body configurations. On the other hand, approaches to topologically quantify amorphous structures such as so-called ring statistics and Voronoi polyhedral analyses have been used in order to characterize atomic configurations of covalent and metallic amorphous solids. However, they require building geometric models based on artificial criteria and do not explicitly extract relevant length scales, turning them not suitable for studying multi-scale phenomena, which are supposed to be important in MRO structures.

The study

Key idea of Nakamura et al 2015 is to apply persistent homology and its graphical representation, the persistence diagram (PD), to atomic configurations, treating the latter as the initial point cloud data. After a brief introduction to persistent homology examples such as the FCC crystal illustrate the geometric meaning of PDs, in this case highlighting the specific features of the crystalline lattice. Persistence diagrams are computed subsequently for the atomic configurations of amorphous silica, obtained from molecular dynamics simulations. The extensivity of Betti numbers, the structural hierarchy of the geometric objects appearing in PDs, and the decomposition method into single atomic components are explained, elucidating the geometry of MRO in amorphous silica.

The results obtained show that persistent homology is a suitable tool to extract many-body atomic structures and to describe MRO geometric features qualitatively, while keeping metric information. The authors conclude that "with the aid of length scales encoded in PDs, hierarchical and multi-scale many-body atomic structures are more successfully represented in an integrated manner compared to existing methods." They "believe that this method also has a great potential to describe the other disordered systems, such as complex molecular liquids, packed granular materials, and metallic glasses."

Keywords

Amorphous materials, medium-range order, atomic configurations, alpha shapes, persistence diagram, Betti numbers

Neurosciences: Towards a new approach to reveal dynamical organization of the brain using TDA

A schematic drawing of an outcoming graph of the Mapper-algorithm.

Introduction

To understand how our brain dynamically adapts from one task to another is crucial for comprehending typical and atypical brain functioning. In addition, the brain's inability to dynamically adjust to environmental demands and brain's aberrant dynamics, on average, have been associated with disorders such as schizophrenia, bipolar disorder, depression and dementia. The high spatiotemporal dimensionality and complexity of neuroimaging data make the study of whole-brain dynamics a challenging endeavor. Often, data is collapsed in time and space early in the analysis, reducing the information content of analysis outcomes.

There is high demand for novel methods that aim for representations of such complex data to discover new aspects within its structures. Particular issues that remain unresolved using usual methodology include uncovering the temporal and spatial scales that best capture clinically and behaviorally relevant brain dynamics, understanding whether the dynamical landscape of possible configurations is best conceptualized as continuous or discrete, and recognizing what constitutes healthy and aberrant dynamics.

The study

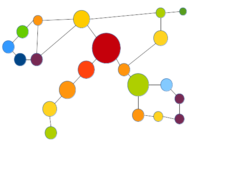
Central feature of the study by Saggar et al 2018 is the application of the TDA algorithm Mapper to represent functional magnetic resonance imaging (fMRI) data in a novel fashion, reducing the high-dimensional datasets into a combinatorial object that attempts to encapsulate the original shape contained in the data. In particular, the mesoscale structure of the obtained shape graphs is studied both graphically and quantitatively, focussing on communities (densely connected nodes within a community, only sparse connection to other communities) and core-periphery structures. The authors tested the efficacy of their approach in an fMRI dataset with known ground truth about the timing of transitions between mental states as dictated by tasks. Rigorous reliability and validation analyses for the proposed approach are included in their study.

Via their approach, novel biological insights could be gained. For instance, participants with a cohesive community structure in their shape graph showed higher performance across different tasks. Thus, suggesting that participants who performed better across tasks had reliably evoked whole-brain configurations that were specific to each task, whereas participants who performed poorly had evoked whole-brain configurations that were more similar between (rather than within) task types. A second biological insight is related to the presence of both community and core-periphery mesoscale arrangements at the level of whole-brain activity maps.

The authors argue, that "... [the obtained] level of detailed representation of transitions in brain configurations makes [their] approach potentially useful in studying brain dynamics in general and developing biomarkers in mental illnesses in particular."

Keywords

Dynamical brain adaption, mental transitions, neuroimaging, fMRI, Mapper, shape graphs, mesoscale arrangements, communities, core-periphery structures

Statistical physics: Persistent homology analysis of phase transitions

Introduction

Phase transitions in statistical systems such as the liquid-gas transition in water are ubiquitous in nature. In recent years, the possibility has been investigated that at least for a broad class of physical systems the deep origin of phase transitions is a major topological change of some submanifolds of the potential configuration space. Key is the idea that the singular energy dependence displayed by the thermodynamic observables at a phase transition is a sign of such major topological changes.

This viewpoint emerged after according to the so-called Yang-Lee theorem the thermodynamic limit of infinitely many particles was necessary for a consistent mathematical framework to describe phase transitions. However, phase transitions such as Bose-Einstein condensation or superconductive transitions can also be observed very far away from the thermodynamic limit. A topological description of phase transitions was developed, although analytic topological information can be obtained only for a very few models.

The study

This is where the study by Donato et al. fits into. It proved useful to investigate topological changes in physical configuration space by identifying their homology from random samples. The authors apply the machinery of persistent homology to two statistical models, from which they know rigorously what to expect: the so-called mean-field [math]XY[/math] model and the lattice [math]\phi^4[/math] model. For the first the topological origin of phase transitions is rigorously ascertained, for the second it is known that the phase transition does not correspond to any topology change in configuration space at a finite number of particles.

Key deduction of the paper is that the persistent homology results match these expectations and can thus be reliably used to further investigate the relationship between topology of configuration space submanifolds and phase transitions.

Keywords

Classical statistical mechanics, phase transitions, mean-field [math]XY[/math] model, [math]\phi^4[/math] lattice model, configuration space topology, persistent homology